Back
1 OUTLINE OF WIND TUNNEL EXPERIMENTS
　　　　The flow, temperature and concentration fields around a building within the non-isothermal boundary layer were selected for this database. The experiment was conducted in the thermally stratified wind tunnel (cross section at measurement part: 1.2 m × 1.0 m) of Tokyo Polytechnic University. The model building had a height (H) of 160 mm, a width (W) of 80 mm, and a depth (D) of 80 mm (H :W :D = 2:1:1), and was located in a turbulent boundary layer as shown in Fig. 1. The temperature conditions of the flow field were set as three cases (Fig.1 and Table 1) of an isothermal (Rb=0.00), a stable non-isothermal state (Rb=0.08), and an unstable non-isothermal state (Rb=-0.10). Fig. 2 shows the vertical distributions of the approaching wind velocity <u>, turbulent kinetic energy k and temperature <θ>. The Reynolds number based on H (building height) and <uH> (approaching wind velocity at building height) was about 15,000. A point gas source was set on the floor 40 mm leeward of the model building. Tracer gas (C2H4: 5% ethylene) was released from a hole (diameter: 5 mm) at a flow rate of q=9.17x10^-6 m3/s. Measurement points were placed at two planes as shown in Fig. 3. The wind velocity, air temperature and gas concentration were simultaneously measured using a split film probe for the wind velocity, a cold-wire for the air temperature and a fast response flame ionization detector for the gas concentration. The sampling frequency was set at 1,000 Hz, to obtain 90,000 data in 90 seconds. Detailed technique for simultaneously measuring fluctuating velocity, temperature and concentration in non-isothermal flow was reported by the present authors [1]. In this wind tunnel experiment, the authors conducted uncertainty analysis [2],[3],[4] to check the reliability of the measurement data. 　
Fig1(a)
(a) Stable Non-isothermal State (Rb=0.08)
Fig1(b)
(b) Isothermal State (Rb=0.00)
Fig1(c)
(c) Unstable Non-isothermal State (Rb=-0.10)
Figure 1 Flow Field Measured for This Database
 
Table 1 Experimental Condition
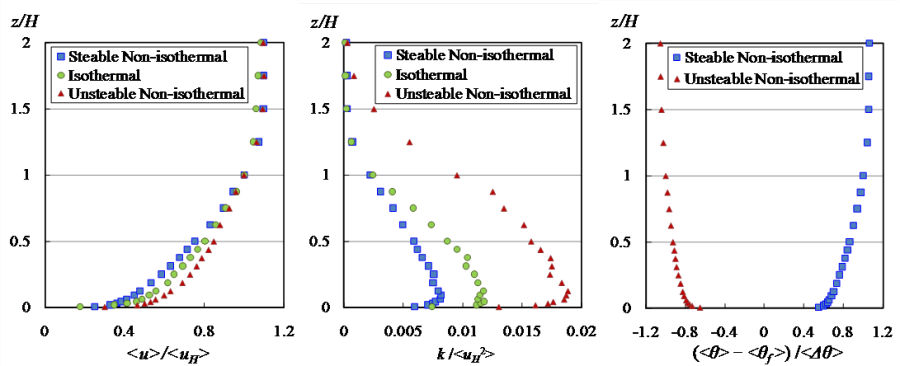
Case (a)
Stable Non-isothermal State		 (b)
Isothermal State		 (c)
Unstable Non-isothermal State
Rb

0.08

0.00

-0.10
H (m)

0.16

0.16

0.16
<uH> (m/s)

1.37

1.40

1.37
<θf > (℃)

17.7

21.2

45.3
<θH> (℃)

49.4

21.5

11.3
<Δθ> (℃)

31.6

0.4

33.9
<θ0> (℃)

41.9

21.5

16.6
<θbuild> (℃)

20.9

21.1

41.7
<θgas> (℃)

31.6

21.2

30.4
 
Fig2
(1) Mean Velocity (2) Turbulent Kinetic Energy (3) Mean Temperature
Figure 2 Inflow Profile without a Model Building (mean value of three measurement lines: x/H=-2.5, 0.0, 2.5)
 
Fig3
Figure 3 Measurement Point Locations
 
2 SYMBOLS
  x, y, z : three components of space coordinates (stream wise, lateral, vertical)
  <ζ> : time averaged variable ζ
  ζ’ : variation of variable ζ, ζ’= ζ－<ζ>
  σζ : standard deviation of variable ζ
  H : building height (0.16 m)
  u, v, w : three components of the velocity vector (m/s)
  usc : scalar velocity, usc= (<u>^2 + <v>^2 + <w>^2)^0.5 (m/s)
  <uH> : <u> value at inflow of computational domain at height H (4.2 m/s)
  θ : air temperature (℃)
  θf : surface temperature of wind tunnel floor (℃)
  θH : air temperature at building hight (℃)
  Δθ : absolute value of temperature difference, Δθ=| θH - θf | (℃)
  θ0 : space averaged air temperature (℃)
  θgas : temperature of released tracer gas (℃)
  θbuild : surface temperature of building model (℃)
  c : gas concentration (ppm)
  cgas : released tracer gas concentration (5.0 x 10^4 ppm)
  q :: released gas emission amount (9.17x10^-6 m3/s)
  c0 : reference gas concentration,c0 = cgas q/<uH>H^2 (ppm)
  Rb : Bulk Richardson number, Rb = gH(<θH>－<θf>) /{(<θ0> +273) <uH^2>}
     
 
3 EXPERIMENTAL DATABASE

　　Data file: Non-Isothermal flow.xlsx -> Download this file (Coming soon...)

　　Wind tunnel experiment result
　　　(1) Mean Wind Velocity: <u>/<uH>
　　　(2) Mean Wind Velocity: <v>/<uH>
　　　(3) Mean Wind Velocity: <w>/<uH>
　　　(4) Mean Scalar Wind Velocity: <usc>/<uH>
　　　(5) Mean Wind Velocity Vector
　　　(6) Normal Stress: <u’^2>/<uH^2>
　　　(7) Normal Stress: <v’^2>/<uH^2>
　　　(8) Normal Stress: <w’^2>/<uH^2>
　　　(9) Turbulent Kinetic Energy : k/<uH^2>
　　　(10) Mean Temperature : (<θ>-<θf >)/<Δθ>
　　　(11) Standard Deviation of Temperature : σθ/<Δθ>
　　　(12) Advection Flux of Temperature : <u>(<θ>-<θf >)/(<uH><Δθ>)
　　　(13) Advection Flux of Temperature : <v>(<θ>-<θf >)/(<uH><Δθ>)
　　　(14) Advection Flux of Temperature : <w>(<θ>-<θf >)/(<uH><Δθ>)
　　　(15) Turbulent Diffusion Flux of Temperature: <u’θ’>/(<uH><Δθ>)
　　　(16) Turbulent Diffusion Flux of Temperature :<v’θ’>/(<uH><Δθ>)
　　　(17) Turbulent Diffusion Flux of Temperature : <w’θ’>/(<uH><Δθ>)
　　　(18) Mean Concentration : <c>/c0
　　　(19) Standard Deviation of Concentration : σc/c0
　　　(20) Advection Flux of Concentration : <u><c>/(<uH>c0)
　　　(21) Advection Flux of Concentration : <v><c>/(<uH>c0)
　　　(22) Advection Flux of Concentration : <w><c>/(<uH>c0)
　　　(23) Turbulent Diffusion Flux of Concentration : <u’c’>/(<uH>c0)
　　　(24) Turbulent Diffusion Flux of Concentration :<v’c’>/(<uH>c0)
　　　(25) Turbulent Diffusion Flux of Concentration : <w’c’>/(<uH>c0)

 
4 REFERENCE
　　[1] R.Yoshie, H.Tanaka, T.Shirasawa,
　　　　Technique for Simultaneous Measurement of Fluctuating Concentration, Velocity and Temperature in Non-isothermal Flow,
　　　　Proceedings of the 12th International Conference on Wind Engineering, pp.1399-1406, July, 2007 [pdf]
　　[2] ISO, Guide to the Expression of Uncertainty in Measurement, 1993.
　　[3] L. Kirkup and B. Frenkel: An introduction to uncertainty in measurement, Cambridge University press, 2006
　　[4] The foundation of modern science and technology from the Physics Laboratory of NIST,
　　　　 http://physics.nist.gov/cuu/Uncertainty/basic.html, (accessed 2005-10-22).
 
5 ACKNOWLEDGEMENT
　　　The following students of Tokyo Polytechnic University assisted us in wind tunnel experiment for this database. We would like to express our heartfelt thanks to them
　　　　・ Mr. Tsuyoshi KOBAYASHI
　　　　・ Ms. Misako WATANABE
　　　　・ Mr. Daisuke UMEZAWA
　　　　・ Mr. Yuki MORI
　　　　・ Mr. Yoshinori KIMURA
　　　　・ Mr. Masanobu TAKEDA
 
6 CONTACT INFORMATION
　　　　Email: yoshie@arch.t-kougei.ac.jp (Prof. Yoshie)
Back
Copyright The 21st Century Center of Excellent Program
Wind Effects on Buildings and Urban Environment, Tokyo Polytechnic University